IBDP Extended Essay and Internal Assessments

As part of the IBDP curriculum, I have written a 4000 word research paper for my Extended Essay in Mathematics. I have also conducted experiments and written reports for Physics and Chemistry as part of the Internal Assessment.

Extended Essay
in Mathematics

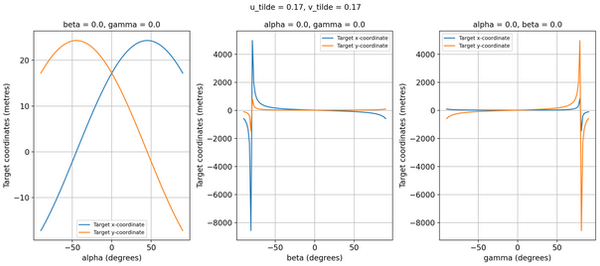
Georeferencing is a function that takes the coordinates of a point on an image and a list of parameters, including the drone’s orientation, height, and camera characteristics, and gives the point’s geographic coordinates as the output. There is already a mathematical process for this, but in my Extended Essay, I explored a method to quantify the sensitivity of the computed geographical coordinates to uncertainties in the parameters of the drone and camera.

Research Question: When using direct georeferencing, to what extent is the accuracy of the computed geographic coordinates affected by uncertainties in the drone's orientation (yaw, pitch, and roll) and variations in position of the target coordinates in the image frame?

Conclusion: I found that the pitch and roll are the most sensitive to uncertainties and sensitivity increases closer to the edges of the image. This knowledge will help make georeferencing more accurate, with implications in fields like urban planning, monitoring natural disasters, and map analysis.

Physics IA

Given the extreme depletion of fossil fuels over the last few decades, it is now more important than ever that we use more renewable energy sources. In my IA, I investigated the effect of blade angle in wind turbines, as finding the optimum angle will help maximize energy production, making wind turbines a more viable option.

Research Question: How does the angle of a wind turbine’s blades affect the rate of rotation of the blades and the power generated by the turbine?

Conclusion: I found that the turbine generates maximum power when all the blade angles are at 3. This is also the blade angle for which the rate of rotation of the blades is highest. The average power output is proportional to the rate of rotation of the turbine’s blades. However, the results also showed that the average power output depends not only on the rate of rotation, but also on the uniformity of the rotation; uniform rotation gives a higher power output than non-uniform rotation when the total blade angle is similar.

Chemistry IA

Indomethacin and Naproxen are common anti-inflammatory drugs used to relieve pain. Metoprolol Succinate is used for the treatment of high blood pressure, and also to prevent chest pain and a second heart attack. Variations in the dissolution rate of the drug in the body can affect its efficacy. When a tablet is swallowed, it has to be absorbed as it passes through the gastro-intestinal tract. The pH in the gastro-intestinal tract can vary based on whether the patient has eaten or not. I used three buffers at different pH to simulate the conditions in the gastro-intestinal tract:

Fasted state, small intestine: Phosphate buffer of pH 6.8
Fed state, small intestine: Acetate buffer of pH 4.6
Fasted state, stomach: HCl buffer of pH 1.2

Research Question: How does the pH of the dissolution media affect the dissolution rate of three drugs - indomethacin, naproxen, and metoprolol succinate?

Conclusion: The dissolution rate and solubility of Indomethacin and Naproxen depended highly on pH, with low solubility at pH1.2 and solubility increasing with pH. Both these drugs are acidic in nature and are BCS Class II, which indicates low solubility. Metoprolol succinate is a highly soluble salt (BCS Class I) and rapidly dissolved in all the pH buffers, showing no variation with pH.

Mathematics IA

The Newton-Raphson Method was made famous by its use in the 3D graphics engine of the Quake III Arena video game, where it is used to compute an accurate estimate of the inverse square root of a positive 32-bit floating-point number, using only a few multiplications and additions (along with some bit-level operations). Importantly, it does not require any floating-point divisions, which are computationally quite expensive. I explored the behaviour of this iteration to find the ideal range of starting points to quickly converge to the required value.

Research Question: How does the function of the Newton iteration for √(1/a) behave for different ranges of starting values?

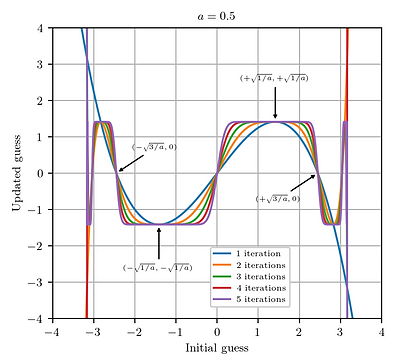
Conclusion: The iteration converges to √(1/a) when the initial guess is between 0 and √(3/a), so this is the ideal range for an initial guess. Clearly, the iteration converges more quickly if the starting value is closer to √(1/a). However, if the initial guess is between √(3/a) and √(5/a), the iteration either gets mapped to 0 or converges to +√(1/a) or - √(1/a) depending on the starting value. If the initial guess is greater than √(5/a), the magnitude of the updated guesses diverges to infinity.